9月10日，我院HUST-UULM中德量子传感与量子测量国际联合实验室蔡建明教授团队在量子传感与精密测量基础理论方面的最新成果以“Quantum Delocalization on Correlation Landscape: The Key to Exponentially Fast Multipartite Entanglement Generation”为题发表在物理学权威期刊《物理评论快报》（Physical Review Letters）上。

量子纠缠作为量子世界最典型的特征之一，是理解许多量子力学基本问题以及发展先进量子技术的核心要素。当前，如何快速有效地制备大规模的多体量子纠缠态，对量子计算、量子通信和量子精密测量等量子技术都具有十分重要的科学意义。例如，大规模多体量子纠缠态的制备时间复杂度一般随着体系规模的增加而增大，进而从根本上制约了量子精密测量所能达到的极限精度。为解决这一问题，研究团队在此前的研究[Phys. Rev. Lett. 130, 170801 (2023) ]中将多体物理中的等效光锥（Lieb-Robinson bound）概念引入量子精密测量,已经建立了多体量子纠缠态制备时间复杂度对量子精密测量精度极限的制约关系，并发现了量子精密测量突破标准量子极限对多体纠缠态制备时间复杂度的基本要求。

然而，由于多体量子物理系统的高度复杂性（描述系统的参数个数随着系统规模的增大而指数性增长），大规模多体量子纠缠态的理论分析与实验制备都仍然面临着诸多严苛的挑战。虽然Lieb-Robinson光锥指出长程相互作用有助于实现多体量子纠缠态的快速制备，但它未能明确指出实现这一目标的具体相互作用形式。如何有效地理解和分析复杂多体量子系统中纠缠增长的动力学，进而实现大规模多体量子纠缠态的快速制备，特别是指数快的制备速度（即制备时间不随着体系的规模增加而增大），是目前亟待解决的难题。系统性解决这一问题，对于推动多体量子物理以及量子信息技术的发展都至关重要。

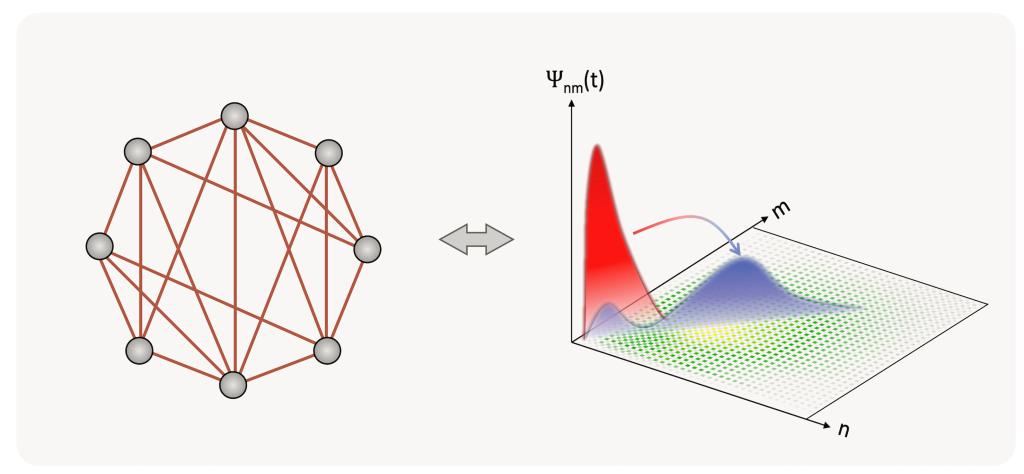
图1.多体系统量子纠缠动力学的非局域化（delocalization）物理图像

为此，研究团队利用量子费舍信息这一物理量度量多体量子态的纠缠度，基于Krylov方法建立了分析量子费舍信息动力学的全新框架。具体地，Krylov空间是描述量子力学算符时间演化的最小完备子空间，在这一子空间中算符可以由一个等效的波函数刻画。从这一思路出发，该团队将量子费舍信息的演化对应为二维波函数在一个关联图景上的非局域化过程，见图1。当波函数传播到关联图景的极大值时，量子费舍尔信息相应也实现了（局部的）最优值。 因而，这一框架建立了量子费舍信息增长与算符波函数非局域化速度之间的深刻联系，而后者由Krylov空间中不同格点耦合系数（即Lanczos系数）的特征决定。特别地，如图2所示当Lanczos系数呈线性增长时，波函数会以指数快的速度发生非局域化，意味着此时量子费舍信息（即体系纠缠度）的增长也是指数快的。

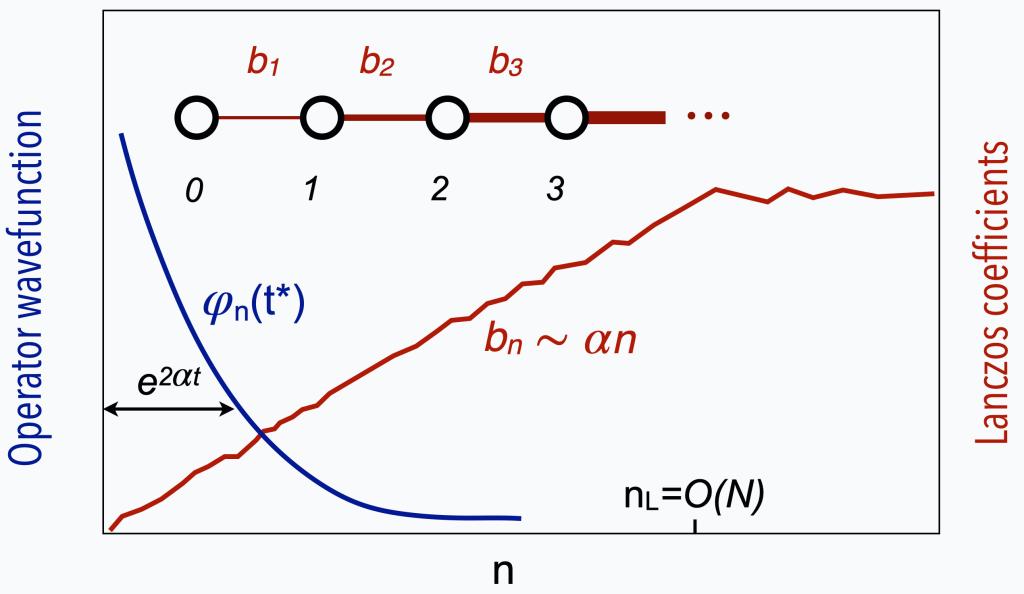
图2. Lanczos系数线性增长特征可以预言量子算符波函数的快速非局域化

研究团队的发现建立了设计多体量子系统快速制备多体量子纠缠态的基本方法，为基于多体量子物理体系制备多体量子纠缠态进而实现量子计算和量子精密测量提供了清晰的物理指引，同时也对理解宏观量子纠缠等量子效应具有重要意义。

物理学院博士后储耀明（物理学院2013级本科生，2017级直博生）为论文的第一作者，博士生李香北（物理学院2016级本科生，2020级直博生）参与该工作，蔡建明教授为通讯作者。此项研究工作获得了国家自然科学基金委、科技部重点研发计划以及中国博士后科学基金的资助支持。

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.110201